答えと解説(5・6年)
問題1 答え:④
(正答率:75%)
この数の列は1,3,5のくり返しで並んでいます。1+3+5=9なので, 1,3,5を1つのグループと考えると,50÷9=5あまり5で,5グループ 目,つまり3×5で,15番目の数までの和が9×5で45になります。 16番目の数の1をたすと45+1=46,17番目の数の3をたすと46+3= 49,18番目の数の5をたすと49+5=54で,初めて50をこえます。
問題2 答え:②
(正答率:85%)
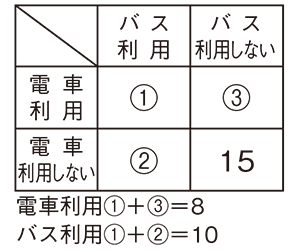
電車かバスのどちらかを利用する人は,30-15で15人です。
ところが,電車を利用する人とバスを利用する人の人数をたすと,8+10で18人になります。
人数が増えているのは電車もバスも利用する人を,電車の方にもバスの方にもふくめて数えているからです。
だから電車とバスの両方を利用する人は,18-15で3人います。
問題3 答え:③
(正答率:50%)
一万円札100枚では100万円です。

10億円は100万円の1000倍だから,高さも1000倍で1000cm,つまり10mになります。
したがって,50億円積むと,高さは50mになります。
問題4 答え:③
(正答率:90%)
おはじきの数は,1番目が3個,2番目が6個,3番目が9個,4番目が12個というように3個ずつ増えていっています。
したがって,5番目は12+3で15個,6番目は15+3で18個,7番目は18+3で21個,8番目は21+3で24個になります。
こうして順に計算してもよいですが,□番目の個数が3×□に等しいことに気づくと,8番目は3×8で24個であり,
たとえば100番目であっても3×100で300個であるとすぐわかります。
問題5 答え:④
(正答率:80%)
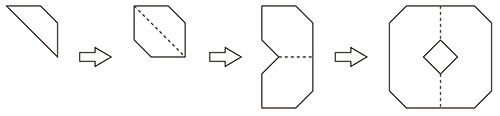
紙を広げていくと,下の図のようになります。
問題6 答え:①
(正答率:60%)
1月10日から数えて1週間後の1月17日が第2回目の特売日になるので,
20回目の特売日は1月10日の19週間後の水曜日です。つまり7×19で133日後です。
1月から始めてそれぞれの月が月末まで何日あるか,順に考えていきましょう。
1月末まで…31ー10=21(日),2月末まで…21+29=50(日),3月末まで…50+31=81(日),4月末まで…81+30=111(日)
133ー111=22(日)なので,20回目は5月22日です。
問題7 答え:③
(正答率:80%)
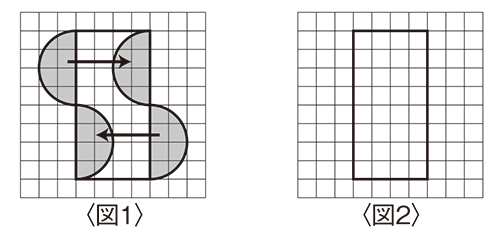
一見複雑そうですが,図1のように半円部分を移動させると図2のような長方形になります。
この長方形は縦8cm,横4cmだから面積は8×4で32cm2です。
問題8 答え:④
(正答率:55%)
5で割り切れる数は,一の位が0か5になります。いちばん大きい整数を作るときは,上の位にできるだけ大きい数を使いましょう。いちばん大きい 整数は750です。いちばん小さい整数を作るときは,上の位にできるだけ小さい数を使いましょう。いちばん小さい整数は205です。その差は,750ー205で545です。
問題9 答え:③
(正答率:85%)
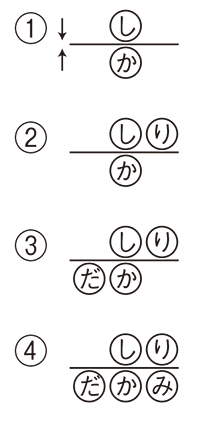
こういった問題では,与えられた条件を図に表したり,表にまとめたりして整理して考えましょう。
①しょうたくんの発言から,しょうたくんとかなさんは机をはさんで向かい合っている。
②りょうくんの右どなりがしょうたくんということは,しょうたくんの左どなりがりょうくんである。
③かなさんの左どなりがだいきくんである。
④りょうくんの向かいがみほさんである。
④の図から,しょうたくんの右どなりはさやかさんであることがわかります。
問題10 答え:④
(正答率:60%)
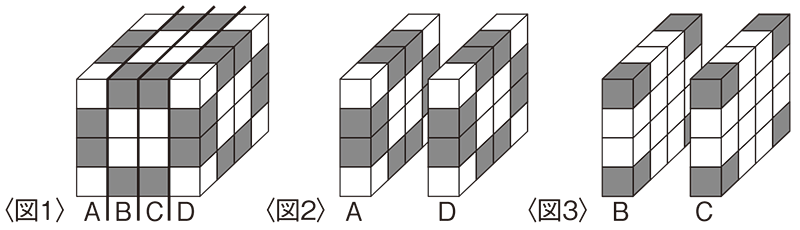
2つの面だけ赤いペンキがぬられているのは図1で の部分の立方体です。
これが何個あるか数えるのに,だぶったり数え落としたりすることのないよう,A,B,C,Dの4つのブロックに分けて考えてみましょう。
図2で外側のA,Dのブロックで8×2の16個です。
図3で内側のB,Cのブロックで4×2の8個,合計16+8で24個になります。